二叉树构造
1、从前序与中序遍历序列构造二叉树
Leetcode 105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
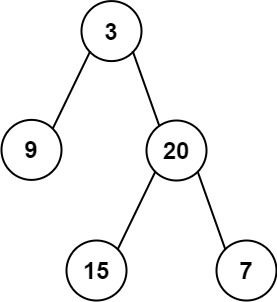
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]提示:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- 3000 <= preorder[i], inorder[i] <= 3000
- preorder 和 inorder 均 无重复 元素
- inorder 均出现在 preorder
- preorder 保证 为二叉树的前序遍历序列
- inorder 保证 为二叉树的中序遍历序列
题目分析
首先我们要知道前序遍历和中序遍历的特点:
- 前序遍历的第一个节点是根节点
- 中序遍历的根节点左边是左子树,右边是右子树
- 通过中序遍历的根节点,我们可以知道左子树的节点个数,右子树的节点个数
具体可以画图来看,比如下面这个例子:
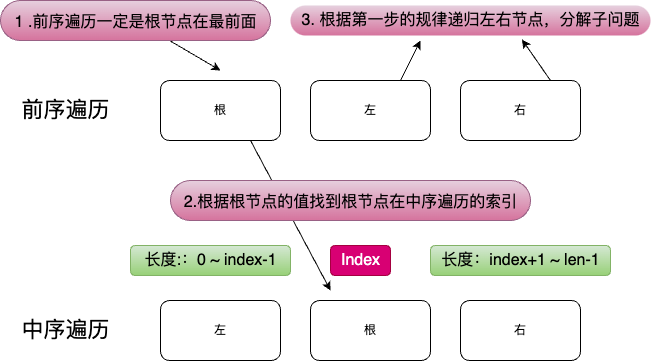
解题思路
有二叉树如下:
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]- 前序遍历第一个节点一定是根节点,也就是 preorder 的 3 一定是第一个节点,
- 但是通过前序遍历我们无法知道左右子树的分界点,这时候中序遍历的作用就体现出来了,节点 3 是根节点,在中序遍历里面, 3 的左边是左子树,右边是右子树,
- 通过中序遍历我们可以知道左子树的节点个数,前序遍历我们可以确定根节点
- 得到子问题左右子树,递归处理,关键点在于如何确定左右子树的范围,答案是通过左右子树的长度去解决
代码实现
var buildTree = function (preorder, inorder) {
// 1. 把需要寻找的数组用 Map 记录 映射关系为:值 => 索引,
// 因为可以从 preOrder 获取根节点,inOrder 肯定在中间,需要找到中间索引,做一个值的映射更好找一些
const inOrderMap = new Map();
for (let i = 0; i < inorder.length; i++) {
inOrderMap.set(inorder[i], i);
}
function build(preL, preR, inL, inR) {
// 递归停止条件
if (preL > preR || inL > inR) return null;
// 头节点的值
const rootValue = preorder[preL];
// rootValue 在 inOrder 的位置
const inorderRootIndex = inOrderMap.get(rootValue);
// 左子树长度
const leftSize = inorderRootIndex - inL;
// 递归 左右子树 找到对应的 preOrder 和 inOrder 分解为子问题
// preL 是根节点 需要 +1 获取子树起点
const left = build(preL + 1, preL + leftSize, inL, inorderRootIndex - 1);
const right = build(preL + leftSize + 1, preR, inorderRootIndex + 1, inR);
// 返回递归后的头节点,并挂载左右子树
return new TreeNode(rootValue, left, right);
}
return build(0, preorder.length - 1, 0, preorder.length - 1);
};2、从中序与后序遍历序列构造二叉树
Leetcode 106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7] 示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder 和 postorder 都由 不同 的值组成postorder 中每一个值都在 inorder 中inorder 保证是树的中序遍历postorder 保证是树的后序遍历
题目分析
题目和上一题后序遍历比较相似
图解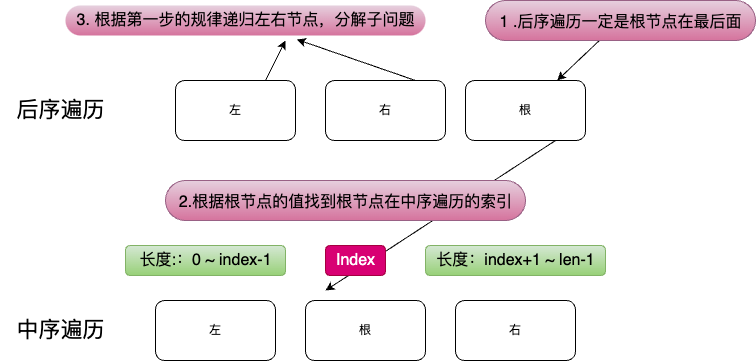
代码实现
var buildTree = function (inorder, postorder) {
// 做一个查找映射
const inOrderIndexMap = new Map();
for (let i = 0; i < inorder.length; i++) {
inOrderIndexMap.set(inorder[i], i);
}
// 分解子问题,得到数组节点
function build(inL, inR, poL, poR) {
// 终止条件是数组越界
if (inL > inR || poL > poR) return null;
// 根据后序遍历的最后一个节点,确定根节点
const root = postorder[poR];
// 找到根节点索引 后序遍历最后一个
const inorderRootIndex = inOrderIndexMap.get(root);
// 左子树长度
const leftTreeSize = inorderRootIndex - inL;
// 递归左右子树,关键是确定左右子树的范围
const leftTree = build(
inL,
inL + leftTreeSize - 1,
poL,
poL + leftTreeSize - 1
);
const rightTree = build(
inorderRootIndex + 1,
inR,
poL + leftTreeSize,
poR - 1
);
// 返回根节点
return new TreeNode(root, leftTree, rightTree);
}
return build(0, inorder.length - 1, 0, postorder.length - 1);
};3、根据前序和后序遍历构造二叉树
LeetCode 889. 根据前序和后序遍历构造二叉树
给定两个整数数组 preorder 和 postorder ,其中 preorder 是二叉树的前序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这棵 二叉树 。
示例 1:
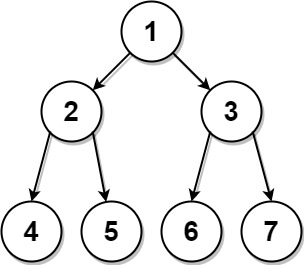
输入:preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1] 输出:[1,2,3,4,5,6,7]
示例 2:
输入: preorder = [1], postorder = [1] 输出: [1]
提示:
1 <= preorder.length <= 301 <= preorder[i] <= preorder.lengthpreorder 中所有值都 不同postorder.length == preorder.length1 <= postorder[i] <= postorder.lengthpostorder 中所有值都 不同保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历
题目分析
和上一题有些区别,前序遍历的第一个节点是根节点,后序遍历的最后一个节点是根节点,需要调整一下思路,在 inorder 中找到左子树的第一元素,在 postorder 中则是最后一个,找到 postorder 对应的 index,就能知道左子树的长度,然后递归处理左右子树;也可以找到右子树长度,然后递归处理左右子树,这是两种不同的答案。
图解
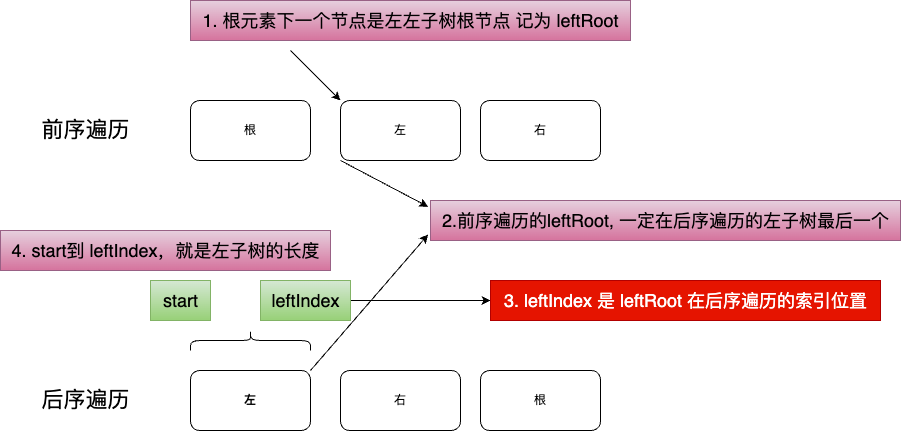
根据上图我们能确定左子树的长度,也能确定右子树的长度,然后递归处理左右子树。
/**
* @param {number[]} preorder
* @param {number[]} postorder
* @return {TreeNode}
*/
var constructFromPrePost = function (preorder, postorder) {
// 依然是把后序遍历数组用 Map 记录 映射关系为:值 => 索引,
// 因为可以从 preOrder 获取左子树根节点位置
const postOrderMapIndex = new Map();
for (let i = 0; i < postorder.length; i++) {
postOrderMapIndex.set(postorder[i], i);
}
function build(preL, preR, postL, postR) {
// 递归停止条件
if (preL > preR || postL > postR) return null;
// 如果相等,说明没有子节点
if (preL === preR) return new TreeNode(preorder[preL]);
// 前序遍历左子树的根节点
const leftRoot = preorder[preL + 1];
// 这个节点在后序遍历的位置
const postLeftIndex = postOrderMapIndex.get(leftRoot);
// 根据位置计算左子树的长度
const leftSize = leftRoot ? postLeftIndex - postL + 1 : 0;
// 递归构造子树
const leftTree = build(preL + 1, preL + leftSize, postL, postLeftIndex);
const rightTree = build(
preL + leftSize + 1,
preR,
postLeftIndex + 1,
postR - 1
);
return new TreeNode(preorder[preL], leftTree, rightTree);
}
return build(0, preorder.length - 1, 0, postorder.length - 1);
};
// @lc code=end